北京化工大学861高等代数与解析几何(无解析与几何)2021年真题
VIP专享
第1页,共 2页
考试年度
研 究 生 入 学 考 试 试 卷
2021
[友情提醒:请在考点提供的专用答题纸上答题,答在本卷或草稿纸上无效!
考试科目代码及名称 高等代数
]
一、填空题 (10 题,每题 3分,共 30 分)
1. 多项式 f(x) = x4−2x+ 5 除以 2x−4所得的余式为 .
2. 设A为3阶方阵,|A|= 2,把A按列分块为 (A1, A2, A3),其中 Aj(j= 1,2,3) 是A的
第j列,则 |A3−2A1, A1,3A2|=.
3. 设A为非奇异矩阵,A∗为A的伴随矩阵,那么 A∗=.
4. 设矩阵 A=2 1
−1 2,E为2阶单位矩阵,矩阵 B满足 BA =B+ 2E,则|B|=.
5. 设α= (1,2,1,3)T, β = (1,0,−1,2)T,那么齐次线性方程组 αβTx= 0 的基础解系包
含 个线性无关的解向量.
6. 已知二次型 f(x1, x2, x3) = ax2
1+ 4x2
2+ax2
3+ 6x1x2+ 2x2x3是正定的,则 a的取值范
围为 .
7. 设V1, V2是V的子空间,dimV1=dimV2=m, dim(V1∩V2) = m−1,则dim(V1+
V2) = .
8. 设3阶矩阵 A的特征值为 2,3, λ.若行列式 |1
2A|= 6,则 λ=.
9. 设α1= (1,2,0,0)T, α2= (0,3,1,0)T, α3= (0,4,0,1)T, α4= (1,5,1,0)T,则向量组
α1, α2, α3, α4的秩等于 .
10. 设A=
1 1 1 1
a1a2a3a4
a2
1a2
2a2
3a2
4
a3
1a3
2a3
3a3
4
,ai̸=aj,(i̸=j, i, j = 1,2,3,4),x=
x1
x2
x3
x4
,B=
1
1
1
1
,则线性方
程组 ATx=B的解用向量表示为 .
二、计算题 (6 题,每题 10 分,共 60 分)
1. 已知 f(x) = x4+x3−3x2−5x−2,g(x) = x3+x2−x−1,(f(x), g(x)) 表示 f(x), g(x)的
首项系数等于 1的最大公因式.计算 (f(x), g(x)),并求 u(x), v(x)使得 (f(x), g(x)) =
u(x)f(x) + v(x)g(x).
1
相关推荐
-
北京工业大学812材料力学2021年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学812材料力学2022年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学822信息与系统2021年真题答案VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学822信息与系统2022年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
兰州大学803半导体物理(含晶体管原理)大学2017年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
兰州大学803半导体物理(含晶体管原理)大学2018年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
兰州大学803半导体物理(含晶体管原理)大学2019年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
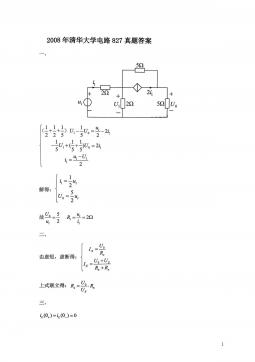
清华大学827电路原理2008年真题答案
 2026-02-26 999+
2026-02-26 999+ -
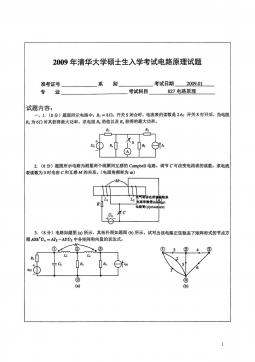
清华大学827电路原理2009年真题
 2026-02-26 999+
2026-02-26 999+ -
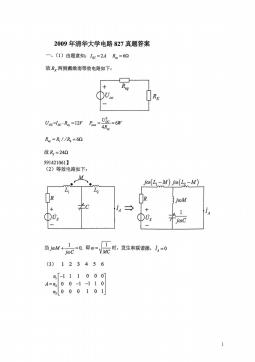
清华大学827电路原理2009年真题答案
 2026-02-26 999+
2026-02-26 999+
作者:平安喜乐
分类:考研考博类
价格:3知币
属性:3 页
大小:246.59KB
格式:PDF
时间:2025-12-29
相关内容
-

厦门大学334新闻与传播专业综合能力2023年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学334新闻与传播专业综合能力2024年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学334新闻与传播专业综合能力2025年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学440新闻与传播专业基础2023年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学440新闻与传播专业基础2024年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币