北京化工大学861高等代数与解析几何2023年样题(学硕)
VIP专享
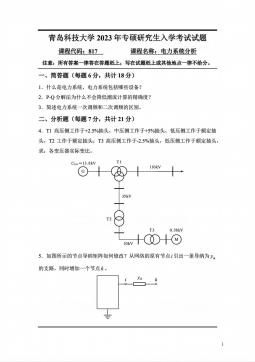
北京化工大学
2002 年攻读硕士学位研究生入学考试
高等代数与解析几何 试题
注意事项
1、答案必须写在答题纸上,写在试卷上均不给分。
2、答题时可不抄题,但必须写清题号。
3、答题必须用蓝、黑墨水笔或圆珠笔,用红色笔或铅笔均不给分。
一、(15 分)证明:若两直线
, l
=+++
=+++
0
0
:
2222
1111
1DzCyBxA
DzCyBxA
l
=+++
=+++
0
0
:
4444
3333
2DzCyBxA
DzCyBxA
相交,则
0
4444
3333
2222
1111
=
DCBA
DCBA
DCBA
DCBA
二、(30 分)
1.判断 z=xy 表示什么曲面。
2.z=xy 是否中心曲面? 若是,求其对称中心。
3.z=xy 有无对称轴? 若有,求其对称轴。
4.z=xy 有无对称平面? 若有, 求其对称平面。
5.z=xy 是否直纹面? 若是,求其直母线族。
三、(30 分)设
P
是数域,
({) }
niPxxxx in
n,,2,1,,,, 21 LL =∈=P 是
数域
P
上的 n维向量空间, 证明: n
P
的每一个真子空间都是数域
P
上某个齐次线性方程组的解空间。
第 页 共3页
1
相关推荐
-
北京工业大学812材料力学2021年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学812材料力学2022年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学822信息与系统2021年真题答案VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学822信息与系统2022年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
兰州大学803半导体物理(含晶体管原理)大学2017年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
兰州大学803半导体物理(含晶体管原理)大学2018年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
兰州大学803半导体物理(含晶体管原理)大学2019年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
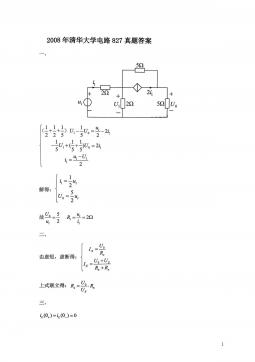
清华大学827电路原理2008年真题答案
 2026-02-26 999+
2026-02-26 999+ -
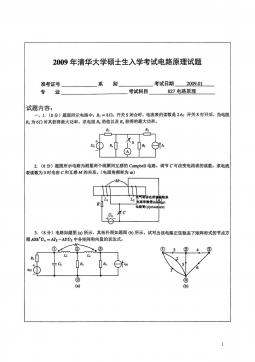
清华大学827电路原理2009年真题
 2026-02-26 999+
2026-02-26 999+ -
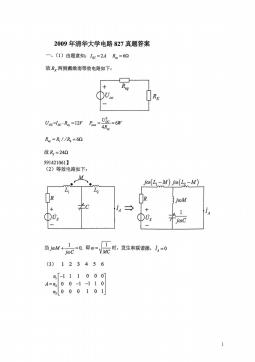
清华大学827电路原理2009年真题答案
 2026-02-26 999+
2026-02-26 999+
作者:平安喜乐
分类:考研考博类
价格:4.9知币
属性:3 页
大小:220.75KB
格式:PDF
时间:2025-12-29
相关内容
-

厦门大学334新闻与传播专业综合能力2023年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学334新闻与传播专业综合能力2024年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学334新闻与传播专业综合能力2025年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学440新闻与传播专业基础2023年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学440新闻与传播专业基础2024年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币