北京交通大学942管理运筹学LP问题解的几种情况在单纯形表上的体现
VIP免费
LP 问题解的几种情况在单纯形表上的体现
赵云平
(临沧师范高等专科学校 数理系,云南 临沧 677099)
摘 要:LP 是线性规划的缩写,LP 问题是运筹学中研究较早、
较成熟的一个分支,
求解 LP 问题的主要算法是单
纯形法。文章基于求解线性规划问题的单纯形法,
讨论了线性规划问题存在唯一最优解、
多重最优解、
无可行解
和无界解在单纯形表上的体现,
完善了线性规划问题解的判别理论。
关键词:LP 问题;单纯形表;解;检验数
收稿日期:2014 - 12 - 02
作者简介:赵云平(1982 - ),
女,
讲师,
硕士,
研究方向为基础数学数论应用、
应用数学运筹学线性规划、
数值代数。
中图分类号:O221. 1 文献标识码:A文章编号:1674-344X(2015)02-0011-03
LP 问题解的几种情形分别是
[1]:唯一解,
即
目标直线的最优位置与可行域边界某个角点相
切;多重最优解,
即目标直线的最优位置与某条约
束直线斜率相同,
刚好与可行域边界的线段重合;
无界解(也称无有限最优解),
即可行域无界,
目标
直线的优化方向向无界方向移动,
永远打不住头,
目标函数趋于无穷大;无可行解,
即各约束无交
集,
可行域为空。在中学阶段,LP 问题解的几种情
形是通过图解法求解来理解的,
图解法也是求解
LP 问题的一种方法,
这种方法仅适用于含有两个
变量的 LP 问题,
实用价值不大。下面主要讨论用
单纯形法求解 LP 问题的过程中,
如何根据单纯形
表判断解的类型(以max 型为例),
并以数值例子
加以说明[2]。
1唯一解
终表中非基变量检验数均小于零,LP 问题有
唯一最优解。
例1用单纯形法求解下列线性规划问题[3]
maxz= 2x1+ 5x2
x1≤4
2x2≤12
3x1+ 2x2≤18
x1,x2≥
0
解:引入松弛变量 x3,x4,x5,
将模型化为标
准型
maxz= 2x1+ 5x2+ 0x3+ 0x4+ 0x5
x1+x3= 4
2x2+x4= 12
3x1+ 2x2+x5= 18
x1,x2,xx,x4,x5≥
0
初始单纯形表:
25000
XBCBB- 1 bx1x2x3x4x5
θ
X30410100—
x40 12 0 (2)0 1 0 6
x50 18 3 2 0 0 1 9
σ25000
第二张单纯形表:
25000
XBCBB- 1 bx1x2x3x4x5
θ
x304101004
x2560101/2 0 —
x50 6 (3)0 0 - 1 1 2
σ2 0 0 - 5 /2 0
终表:
25000
XBCBB- 1 bx1x2x3x4x5
θ
x3020011/3 - 1 /3
x2560101/2 0
x122100-1/3 1 /3
σ0 0 0 - 11 /6 - 2 /3
终表检验数 σ均小于等于零,
当前解为最优
相关推荐
-
北京工业大学812材料力学2021年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学812材料力学2022年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学822信息与系统2021年真题答案VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学822信息与系统2022年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
兰州大学803半导体物理(含晶体管原理)大学2017年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
兰州大学803半导体物理(含晶体管原理)大学2018年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
兰州大学803半导体物理(含晶体管原理)大学2019年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
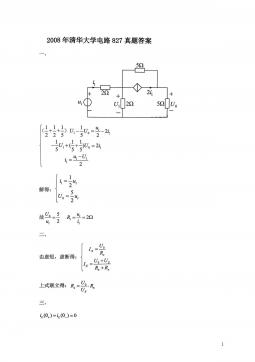
清华大学827电路原理2008年真题答案
 2026-02-26 999+
2026-02-26 999+ -
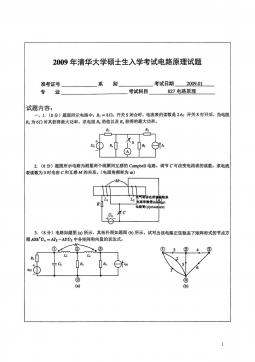
清华大学827电路原理2009年真题
 2026-02-26 999+
2026-02-26 999+ -
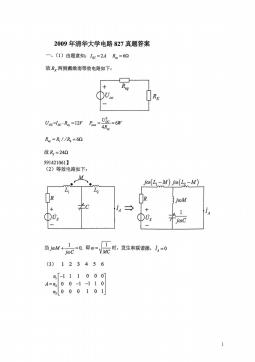
清华大学827电路原理2009年真题答案
 2026-02-26 999+
2026-02-26 999+
作者:平安喜乐
分类:考研考博类
价格:1知币
属性:4 页
大小:296.11KB
格式:PDF
时间:2025-12-31
相关内容
-

宁夏大学电路手写版答案
分类:考研考博类
时间:2026-02-26
标签:无
格式:PDF
价格:免费
-
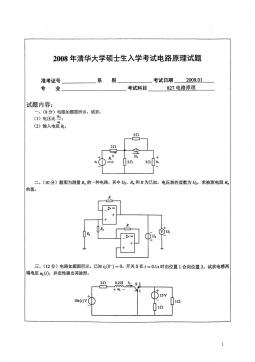
清华大学827电路原理2008年真题
分类:考研考博类
时间:2026-02-26
标签:清华大学
格式:PDF
价格:免费
-

清华大学827电路原理2008年真题答案
分类:考研考博类
时间:2026-02-26
标签:清华大学
格式:PDF
价格:免费
-

清华大学827电路原理2009年真题
分类:考研考博类
时间:2026-02-26
标签:清华大学
格式:PDF
价格:免费
-

清华大学827电路原理2009年真题答案
分类:考研考博类
时间:2026-02-26
标签:清华大学
格式:PDF
价格:免费