温州大学618数学分析2012年真题
标签: #真题
相关推荐
-
北京工业大学812材料力学2021年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学812材料力学2022年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学822信息与系统2021年真题答案VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学822信息与系统2022年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
兰州大学803半导体物理(含晶体管原理)大学2017年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
兰州大学803半导体物理(含晶体管原理)大学2018年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
兰州大学803半导体物理(含晶体管原理)大学2019年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
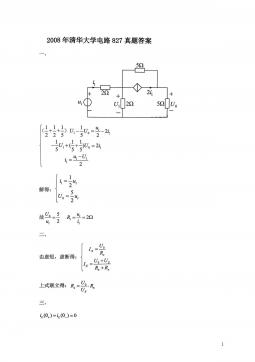
清华大学827电路原理2008年真题答案
 2026-02-26 999+
2026-02-26 999+ -
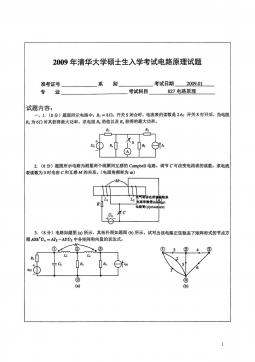
清华大学827电路原理2009年真题
 2026-02-26 999+
2026-02-26 999+ -
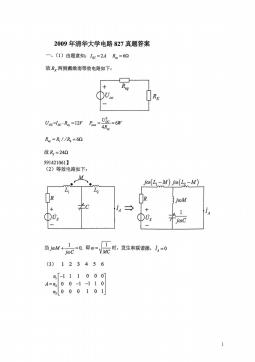
清华大学827电路原理2009年真题答案
 2026-02-26 999+
2026-02-26 999+
相关内容
-

厦门大学334新闻与传播专业综合能力2023年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学334新闻与传播专业综合能力2024年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学334新闻与传播专业综合能力2025年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学440新闻与传播专业基础2023年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学440新闻与传播专业基础2024年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币











