温州大学618数学分析2006年真题
免费
温州大学 2006年考研数学分析试题
1、( 15 分)设
Axf
ax
)(lim
,
Bxg
Ax
)(lim
而且在某
)(
0aU
内
Axf )(
.
(1)求证:
Bxfg
ax
))((lim
;
(2)举例说明去掉条件“在某
)(
0aU
内
Axf )(
”结论(1)不成立.
2、( 20 分)(1)求证:
0x
时
xx
xf 1
sin
1
)(
是无界量但不是无穷大量.
(2)设
)(xf
在
],[ ba
上连续,
*
x
是
)(xf
在
],[ ba
上唯一的最大值点.如果
],[}{ baxn
使
得
)()(lim *
xfxf n
n
,求证:
*
lim xxn
n
.
3、( 18 分)设
0 ,0
0,
1
sin
)(
x
x
x
x
xf
m
.试确定整数
m
的取值范围,使得
(1)
)(xf
在
0x
处连续;
(2)
)(xf
在
0x
处可导;
(3)
)(xf
在
0x
处连续.
4、( 20 分)(1)设
)(xf
在
],[ ba
上连续,
)(xf
在
),( ba
中存在而且
0)()( bfaf
.求
证:存在
),( ba
使得
)()(
ff
.
(2)试求方程
xx sin2
在闭区间
]2,0[
上的解.
5、( 12 分)设
)(xf
在
]1,0[
上可微,
0)0( f
而且当
)1,0(x
时,
1)(0
xf
.求证:
1
0
3
2
1
0 )())(( dxxfdxxf
.
6、( 15 分)(1)设
0
n
a
)1( n
.求证:
n
na
1
与
n
n
na
a
1
1
具有相同的敛散性.
(2)讨论级数
3
cos)1( 2
1
n
n
nn
a
n
(其中
a
为常数)的敛散性.
7、( 16 分)(1)试构造一个二元函数,使它在原点处可微但偏导数不连续,并加以说明.
(2)设由
),( yxfz
,
)(xyyx
所确定的隐函数
)(xzz
可微,试求
dx
dz
.
标签: #真题
相关推荐
-
北京工业大学812材料力学2021年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学812材料力学2022年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学822信息与系统2021年真题答案VIP专享

 2025-12-29 999+
2025-12-29 999+ -
北京工业大学822信息与系统2022年真题VIP专享

 2025-12-29 999+
2025-12-29 999+ -
兰州大学803半导体物理(含晶体管原理)大学2017年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
兰州大学803半导体物理(含晶体管原理)大学2018年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
兰州大学803半导体物理(含晶体管原理)大学2019年真题VIP免费

 2025-12-31 999+
2025-12-31 999+ -
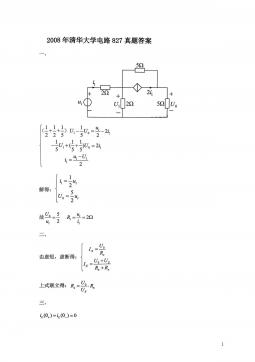
清华大学827电路原理2008年真题答案
 2026-02-26 999+
2026-02-26 999+ -
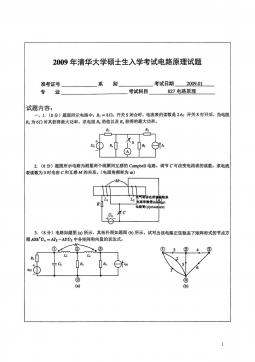
清华大学827电路原理2009年真题
 2026-02-26 999+
2026-02-26 999+ -
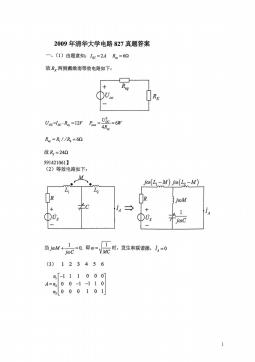
清华大学827电路原理2009年真题答案
 2026-02-26 999+
2026-02-26 999+
作者:北木在北
分类:考研考博类
价格:免费
属性:3 页
大小:276.79KB
格式:PDF
时间:2026-01-04
相关内容
-

厦门大学334新闻与传播专业综合能力2023年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学334新闻与传播专业综合能力2024年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学334新闻与传播专业综合能力2025年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学440新闻与传播专业基础2023年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币
-

厦门大学440新闻与传播专业基础2024年真题
分类:考研考博类
时间:2026-02-26
标签:真题
格式:PDF
价格:4.9 知币











